解答です。
設問1
[a]:ア [b]:オ [c]:ウ [d]:イ
設問2
設問3
[e]:カ [f]:コ [g]:キ [h]:ク [I]:ウ [j]:コ
解説してみた。
設問1
稼働率の計算ですが、稼働率でなく故障率が与えられているので、多少ややこしいです。
(1)サブシステム1は、Webサーバが2つ並列のシステム構成になってます。
Webサーバが2つ並列に並んでいる場合の稼働率は、2つのWebサーバが同時に故障しなければOKなので、1から2つのWebサーバが同時に故障する確率を引いたものになるので、サブシステム1稼働率p1は1-fweb2となります。よって、[a]には「ア」(1-fweb2)が入ります。
(2)直列に接続されているDBサーバと磁気ディスク装置1組の稼働率は、DBサーバの稼働率×磁気ディスク装置の稼働率になります。稼働率は1-故障率なので、DBサーバと磁気ディスク装置1組の稼働率p2は(1-fdb)(1-fhd)になります。よって、[b]には「オ」((1-fdb)(1-fhd))が入ります。
解答群を見ると、サブシステム2全体の稼働率は、p2を使って求めればOKになってます。サブシステム2は、直列に接続されているDBサーバと磁気ディスク装置の組(稼働率p2)が並列に接続されていることから、稼働率は1-(1-p2)2になります。よって、[c]には「ウ」(1-(1-p2)2)が入ります。
(3)検討案1のシステムは、サブシステム1とサブシステム2が直列に接続されたシステムなので、稼働率は、サブシステム1の稼働率p1×サブシステム2の稼働率p3になります。よって、[d]には「イ」(p1p3)が入ります。
設問2
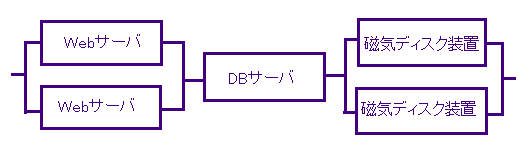
検討案2は、「並列のWebサーバ2台」「DBサーバ1台」「並列の磁気ディスク装置2台」の各組が直列に接続された構成になっています。よって、検討案2の信頼性モデル図は、設問2の解答の所にある図になります。
設問3
Webサーバ、DBサーバ、磁気ディスク装置の故障率が全てfなので、検討案2の稼働率は、
(1-f2)×(1-f)×(1-f2)
になります。
fの故障率1/2をhとした場合、
改良案1の稼働率:(1-h2)×(1-f)×(1-f2)
改良案2の稼働率:(1-f2)×(1-h)×(1-f2)
改良案3の稼働率:(1-f2)×(1-f)×(1-h2)
となります。
改良案1/改良案2の稼働率は、
{(1-h2)×(1-f)×(1-f2)}/{(1-f2)×(1-h)×(1-f2)}
です。(1-f2)=(1+f)(1-f)、(1-h2)=(1+h)(1-h)となることを利用して式を整理すると、
(1+h)/(1+f)
になります。h=f/2なので、
(1+f/2)/(1+f)
です。fに0<f<1となるような適当な数値を代入すると、分母の方が大きくなるため、稼働率は改良案1より改良案2の方が高くなります。よって、[e]には「カ」((1+f/2)/(1+f))、[f]には「コ」(改良案2の方が高い)が入ります。
改良案1/改良案3の稼働率は、
{(1-h2)×(1-f)×(1-f2)}/{(1-f2)×(1-f)×(1-h2)}
です。分子と分母の構成要素が同じなので、式を整理すると1になり、改良案1と改良案3は稼働率が同じになります。よって、[g]には「キ」(1)、[h]には「ク」(同じである)が入ります。
改良案2/改良案3の稼働率は、
{(1-f2)×(1-h)×(1-f2)}/{(1-h2)×(1-f)×(1-f2)}
です。ちょうど、改良案1/改良案2の分子と分母を入れ替えた構成なので、式を整理すると、
(1+f)/(1+h)
になります。h=f/2なので、
(1+f)/(1+f/2)
です。fに0<f<1となるような適当な数値を代入すると、分子の方が大きくなるため、稼働率は改良案3より改良案2の方が高くなります。よって、[e]には「ウ」((1+f)/(1+f/2))、[f]には「コ」(改良案2の方が高い)が入ります。
IPAの公式解答はこちら。
平成17年秋ソフトウェア開発技術者午後1 IPA公式解答(PDFファイル)
今回は、信頼性モデル図を書く以外は、解答群の中から記号で選択して解答する形式でした。
システムアーキテクチャー(情報システム構成)分野では、システムの信頼性を評価するための稼働率計算は定番中の定番ですが、今回は故障率を使っての稼働率計算だったので、故障率から稼働率への変換が面倒でした。それから、設問3の稼働率計算は、 (1-f2)=(1+f)(1-f)ができないと解答にたどり着けないので、 中学~高校の数学を忘れてしまった方にはきつそうです。