サービス窓口が３つの待ち行列の計算。（平成16年春ソフトウェア開発技術者午後１問４）

解答です。

(1)

(2)[a]:10　[b]:0.07　[c]:0.7　[d]:0.04　[e]:1.22　[f]:71.22

(3)[g]:到着順　[h]:長く

解説してみた。

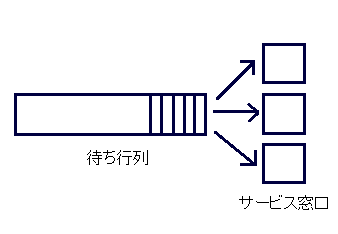
(1)M／M／3モデルは、待ち行列１列に対して、サービス窓口が３つあるモデルです。待ち行列の先頭に来たら、到着順に３つの窓口に割り振られます。よって、「解答です。」の(1)のような模式図になります。

(2)
・[a]，[b]，[c]について
　文中に「アクセス件数は1 秒当たり平均10 件，アクセス1 件の平均処理時間は70 ミリ秒」とあるので、λ＝10(／秒），t_s＝0.07（秒）となります。そして、トラフィック密度u＝λt_sなので、u=0.7になります。よって、[a]には「10」、[b]には「0.07」、[c]には「0.7」が入ります。
・[d]について
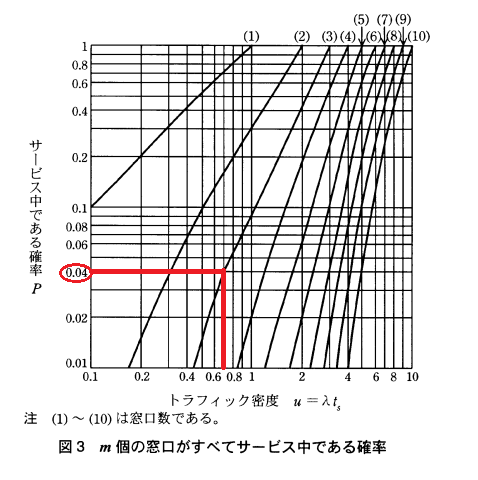
　窓口数は３なので、(3)の曲線を使用します。 トラフィック密度 u＝λt_s＝0.7なので、(3)の曲線が0.7のときのPの値は0.04になってます。よって、[d]には「0.04」が入ります。

・[e]について
　平均待ち時間は、Pt_s／(m－λt_s)の式で計算できるので、数値を当てはめて計算して小数第2 位まで求めると、

0.04×0.07／(3－0.7)＝0.0028／2.3＝1.22×10^-3（秒）

になります。待ち時間はミリ秒で求めるので、[e]には1.22が入ります。
・[f]について
待ち時間を含めた平均処理時間＝待ち時間＋平均処理時間で、[e]で求めた待ち時間が1.22ミリ秒、平均処理時間が70ミリ秒なので、待ち時間を含めた平均処理時間は71.22ミリ秒になります。よって、[f]には「71.22」が入ります。

(3)
・[g]，[h]について
　待ち行列理論では、ランダムにサービス要求が到着して待ち行列に並ぶとともに、サービス窓口が到着順を守ってサービス要求を処理します。それに対してA社のシステムは、サーバの負荷状態に応じて１分ごとに最も負荷が少ないWebサーバにアクセスを振り分けることから、１列の待ち行列が３つに分割され、「待ち行列１つ、サービス窓口１つ」が３つ作られることになります。

　そうなると、必ずしもサービス要求（今回はアクセス要求）の到着順にサービスが処理されるとは限らないです。

　利用率が同じ場合、「待ち行列n列、サービス窓口n個」のモデルの方が、「待ち行列１列、サービス窓口n個」のモデルよりも、平均待ち時間が長くなります。詳細は、こちらの記事で解説されています。よって、[g]には「到着順」、[h]には「長く」が入ります。

IPAの公式解答
平成16年春ソフトウェア開発技術者午後１　IPA公式解答（PDFファイル）

　問３に引き続き、問４も情報システムについての計算問題になってました。グラフを読み取りながら、手順に従って待ち行列についての数値を求めていきます。計算が面倒だったことに加え、「待ち行列１列、サービス窓口n個」（M／M／n）と「待ち行列n列、サービス窓口n個」（M／M／1が３つ）の違いの把握がなかなか難しい。